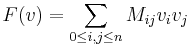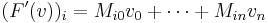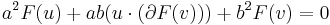Quadric (projective geometry)
In projective geometry a quadric is the set of points of a projective space where a certain quadratic form on the homogeneous coordinates becomes zero. It may also be defined as the set of all points that lie on their dual hyperplanes, under some projective duality of the space.
Contents |
Formal definition
More formally, let  be an
be an 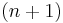 -dimensional vector space with scalar field
-dimensional vector space with scalar field  , and let
, and let  be a quadratic form on
be a quadratic form on  . Let
. Let  be the
be the  -dimensional projective space corresponding to
-dimensional projective space corresponding to  , that is the set
, that is the set ![\{ [v]\;�:\; v \in V \setminus \{0\} \}](/2012-wikipedia_en_all_nopic_01_2012/I/7349c3e5d05184336e9a6f612a5ad509.png) , where
, where ![[v]](/2012-wikipedia_en_all_nopic_01_2012/I/ffc86d011359d705c53201cf057f7662.png) denotes the set of all nonzero multiples of
denotes the set of all nonzero multiples of  . The (projective) quadric defined by
. The (projective) quadric defined by  is the set of all points
is the set of all points ![[v]](/2012-wikipedia_en_all_nopic_01_2012/I/ffc86d011359d705c53201cf057f7662.png) of
of  such that
such that 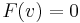 . (This definition is consistent because
. (This definition is consistent because ![[u] = [v]](/2012-wikipedia_en_all_nopic_01_2012/I/b3d2b6f2d750e0f59552643a474a40cc.png) implies
implies 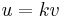 for some
for some 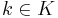 , and
, and 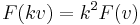 by definition of a quadratic form.)
by definition of a quadratic form.)
When  is the real or complex projective plane, the quadric is also called a (projective) quadratic curve, conic section, or just conic.
is the real or complex projective plane, the quadric is also called a (projective) quadratic curve, conic section, or just conic.
When  is the real or complex projective space, the quadric is also called a (projective) quadratic surface.
is the real or complex projective space, the quadric is also called a (projective) quadratic surface.
In general, if  is the field of real numbers, a quadric is an
is the field of real numbers, a quadric is an 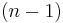 -dimensional sub-manifold of the projective space
-dimensional sub-manifold of the projective space  . The exceptions are certain degenerate quadrics that are associated to quadratic forms with special properties. For instance, if
. The exceptions are certain degenerate quadrics that are associated to quadratic forms with special properties. For instance, if  is the trivial or null form (that yields 0 for any vector
is the trivial or null form (that yields 0 for any vector  ), the quadric consists of all points of
), the quadric consists of all points of  ; if
; if  is a definite form (everywhere positive, or everywhere negative), the quadric is empty; if
is a definite form (everywhere positive, or everywhere negative), the quadric is empty; if  factors into the product of two non-trivial linear forms, the quadric is the union of two hyperplanes; and so on. Some authors may define "quadric" so as to exclude some or all of these special cases.
factors into the product of two non-trivial linear forms, the quadric is the union of two hyperplanes; and so on. Some authors may define "quadric" so as to exclude some or all of these special cases.
Matrix representation
Any quadratic form  can be expressed as
can be expressed as
where 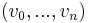 are the coordinates of
are the coordinates of  with respect to some chosen basis, and
with respect to some chosen basis, and  is a certain
is a certain 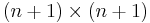 symmetric matrix with entries
symmetric matrix with entries 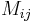 in
in  , that depends on
, that depends on  and on the basis.
and on the basis.
This formula can also be written as 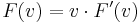 where
where  is the standard inner product of
is the standard inner product of 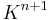 , and
, and 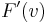 is the vector of
is the vector of 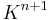 defined by
defined by
The quadratic form  is trivial if and only if all the entries
is trivial if and only if all the entries 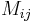 are 0. If
are 0. If  is the real numbers, there is always a basis such that
is the real numbers, there is always a basis such that  is a diagonal matrix. In this case, the signs of the diagonal elements
is a diagonal matrix. In this case, the signs of the diagonal elements 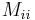 determine whether the quadric is degenerate or not.
determine whether the quadric is degenerate or not.
Polarity, tangent hyperplane, and singular points
In general, a projective quadric  defines a projective polarity: a mapping that takes any point
defines a projective polarity: a mapping that takes any point ![p=[v]](/2012-wikipedia_en_all_nopic_01_2012/I/6419f747baac48fa17e9e190dd324126.png) of
of  to a hyperplane
to a hyperplane 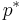 of
of  , and vice-versa, while preserving the incidence relation between points and hyperplanes. The coefficient vector of the polar hyperplane
, and vice-versa, while preserving the incidence relation between points and hyperplanes. The coefficient vector of the polar hyperplane 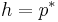 , relative to the chosen basis of
, relative to the chosen basis of  , is
, is 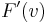 .
.
If  is not on the quadric, the hyperplane
is not on the quadric, the hyperplane 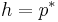 is well-defined (that is, not identically zero) and does not contain
is well-defined (that is, not identically zero) and does not contain  .
.
If  is on the quadric and the hyperplane
is on the quadric and the hyperplane 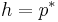 is well-defined, and contains
is well-defined, and contains  (which is said to be a regular point). In fact, it is the hyperplane that is tangent to the quadric at
(which is said to be a regular point). In fact, it is the hyperplane that is tangent to the quadric at  .
.
If  is on the quadric, it may happen that all coefficients
is on the quadric, it may happen that all coefficients 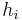 are zero. In that case the polar
are zero. In that case the polar 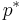 is not defined, and
is not defined, and  is said to be a singular point or singularity of the quadric.
is said to be a singular point or singularity of the quadric.
The tangent hyperplane turns out to be the union of all lines that are either entirely contained in  , or intersect
, or intersect  at only one point.
at only one point.
The condition for a point ![[u]](/2012-wikipedia_en_all_nopic_01_2012/I/2c4cf6962f885c2c75ab11ce45063565.png) to be in the hyperplane that is tangent to
to be in the hyperplane that is tangent to  at
at ![[v]](/2012-wikipedia_en_all_nopic_01_2012/I/ffc86d011359d705c53201cf057f7662.png) is
is 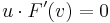 , which is equivalent to
, which is equivalent to 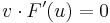
The condition for a point ![[v]](/2012-wikipedia_en_all_nopic_01_2012/I/ffc86d011359d705c53201cf057f7662.png) to be singular is
to be singular is 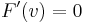 . The quadric has singular points if and only the matrix
. The quadric has singular points if and only the matrix  , in diagonal form, has one or more zeros in its diagonal. It follows that the set of all singular points on the quadric is a projective subspace.
, in diagonal form, has one or more zeros in its diagonal. It follows that the set of all singular points on the quadric is a projective subspace.
Intersection of lines with quadrics
In projective space, a straight line may intersect a quadric  at zero, one, or two points, or may be entirely contained in it. The line defined by two distinct points
at zero, one, or two points, or may be entirely contained in it. The line defined by two distinct points ![p=[u]](/2012-wikipedia_en_all_nopic_01_2012/I/a9442ee78d68516c3f02f8a0ab452281.png) and
and ![q=[v]](/2012-wikipedia_en_all_nopic_01_2012/I/7952bbcaa38f5639885b56ae652c12e9.png) is the set of points of the form
is the set of points of the form ![[a u %2B b v]](/2012-wikipedia_en_all_nopic_01_2012/I/a9e9ee751ca3c8dbd218eaf184316715.png) where
where 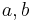 are arbitrary scalars from
are arbitrary scalars from  , not both zero. This generic point lies on
, not both zero. This generic point lies on  if and only if
if and only if 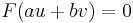 , which is equivalent to
, which is equivalent to
The number of intersections depends on the three coefficients 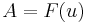 ,
, 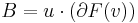 , and
, and 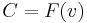 . If all three of
. If all three of 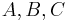 are zero, any pair
are zero, any pair 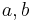 satisfies the equation, so the line is entirely contained in
satisfies the equation, so the line is entirely contained in  . Otherwise, the line has zero, one, or two distinct intersections depending on whether
. Otherwise, the line has zero, one, or two distinct intersections depending on whether 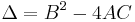 is negative, zero, or positive, respectively.
is negative, zero, or positive, respectively.